Note : Cet article en français
Foreword: this article is about music theory, explained to non-musicians and musicians alike, with very simple math (all you need is basic fractions). Unless you know Werckmeister and Valotti, you will definitely learn something cool from this article. 🙂
Musicians have always had to tune their instruments to avoid having their audience’s ears bleeding. This is not only true for an organ that has 20,000+ pipes. One of the simplest instruments, a flute made of a stick of bamboo (or a bone, can you think of anything more romantic than playing your favorite tune on your sweetheart’s tibia?… just kidding) with holes in it has to be constructed very carefully: move a hole by a single millimeter, your flute will sound out of tune.

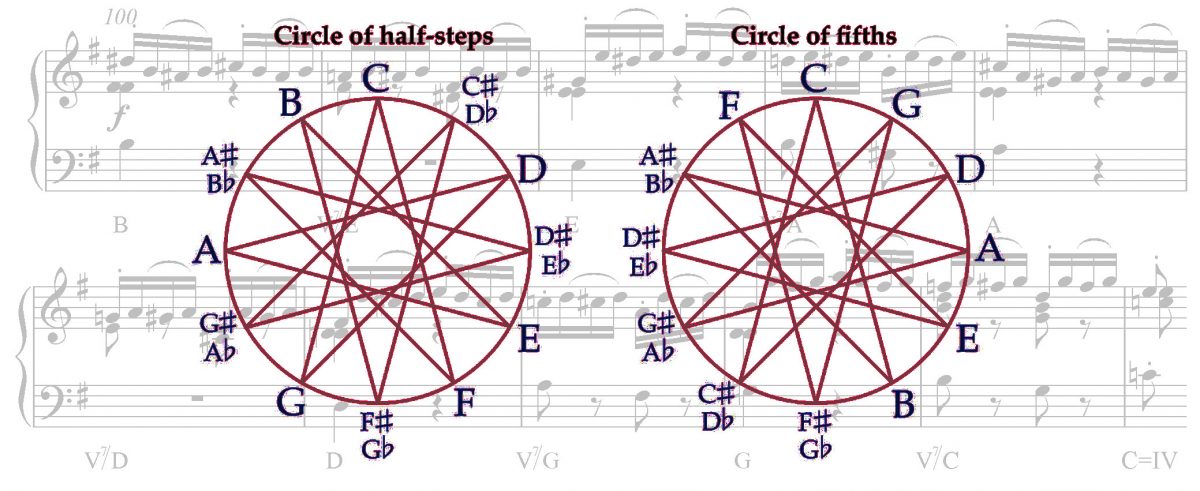
2500 years ago, Pythagoras, with the limited instruments of the time, racked his brain on the problem of tuning and finally devised the “circle of fifths”, exposing the impossibility to tune any instrument perfectly:

Pythagoras understood that music is essentially mathematics: notes, harmonics, pitches are all about different frequencies and how these frequencies interact with each other. Our brains and ears recognize matching frequencies as harmonious and non matching frequencies as dissonant. In fact, the brain loves everything that is mathematically related. That is why we love symmetries such as these:

Back to music. When two notes are played together, they form an “interval”, which is the distance between their respective frequencies. Intervals sound great to the ear when the frequencies of the two notes composing the interval are mathematically related by integer fractions. If they are out of tune and too far from a perfect ratio, they start sounding bad. Besides, any listener will hear “beats” as soon as the interval is a little off, which makes it easier to tune perfect intervals with a very good precision, the ear is a very delicate and precise organ.
Let’s hear what it sounds like! I have recorded a simple fifth, C-G, on my spinet, an instrument that has only one string per note, which makes hearing things more simple. First, let’s listen to a fifth that has been perfectly tuned, it sounds regular, fading away slowly (for best results, use a headset):
Visually, the sound wave is a gradually decreasing sound:

Now when this fifth starts getting out of tune, it starts “beating”, follow the visual indication. If needed, play the video a couple of times until you clearly hear the beats:
The beats clearly show on the audio wave:

Finally, when the fifth is clearly out of tune, the beats get faster, note that this is not a digital sound effect, this is exactly how it sounds on my spinet:
And when looking at the sound wave, the beats are even more visible:

And the only thing I did was to change the G very slightly, actually less than 1% of its perfect value!
Now, let’s have a look at the different perfect intervals that can be formed.
| Take a frequency and its double: you have an octave. For instance 440 Hz and 880 Hz. |  |
| Now take 3/2 of a frequency, you have a harmonious fifth. |  |
| Take the 4/3, you get a fourth. |  |
| 5/4, a major third. |  |
| 6/5, a minor third. |  |
Remember, as soon as two notes don’t respect these perfect intervals, they start sounding “off” and their combination starts “beating”.
So far, so good, everything looks pretty simple, we just need to tune our instrument using perfect intervals, et voilà!
But here comes the problem: it is mathematically impossible to slice an octave into 12 notes (called semitones) that have perfect fifths, forget even about perfect fourth or thirds. This assertion might sound blunt. We need proof! Let’s dig into the problem.
An octave is generally very “round” to the ear. It’s the combination of a frequency and its double, the brain is very satisfied with that. In fact, when tuned correctly, it is even sometimes difficult to say that there are actually two notes there, they “blend” perfectly. Can you hear the two notes here making an octave:
With his circle of fifths, Pythagoras proved that, if you wanted to tune your instruments so that it would have perfect fifths, your octave would sound like this:
Ouch! Your ears could do with some little extra care now. You can listen to the perfect octave above to get away from this annoying sound ringing in your ear. While Pythagoras used many fifths and octaves to prove this, we can actually use just 5 notes to demonstrate it.
Let’s calculate how much we have between C and D if we want to maintain things perfect. C-G is a fifth, so it is a 3/2 interval, as we have seen in the table just above. This means that G is 3/2 of C. D-G is a fourth, so it is a 4/3 interval. Which means that to go from G down to D, we have to divide by 4/3:

G = C × 3/2
D = G ÷4/3 = G × 3/4 = (C × 3/2) × 3/4 = C × 9/8
So D is 9/8 of C when building it with perfect intervals. Great. This is just simple math, jumping from one note to the other using basic fractions.

Now, let’s see what we have between C and E. E must also be 9/8 of D, as it is a normal tone in the scale, no different than C-D.

So E must mathematically be 81/64 of C. And 81/64 ≈ 1.265. Wait a second. C-E is a major third. We have said earlier that perfect major thirds use a 5/4 interval. However, 5/4 = 1.25, not 1.265. Close. But not exact. That’s our first “uh-oh” problem: when we use perfect intervals to build the interval C-D, we can no longer create perfect intervals for the major third C-E, and you can guess that it will also be the case with other intervals.
For instance, let’s go on to the next octave using 9/8 as a step for a tone. C -> D is 9/8, C -> E is 9²/8² (9/8 times 9/8), C -> F# is 9³/8³, etc.:
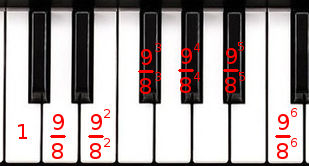
So an octave constructed with 6 tones is actually 9⁶/8⁶ ≈2.0273. But we said an octave needs to have a ratio of 2 to sound perfect, not 2.0273. Oh well, here goes perfection in music! And you heard what 2.0273 instead of 2 sounds like before, it’s simply horrible! Let’s play it again:
At this point, we have to accept one fact that is hard to swallow: dividing an octave into 12 notes is never going to produce exact fifths, fourths or thirds. Very close approximations of them, but never exact. However you tune your notes, they will never sound perfect. Such an annoying thought for a musician! However perfect his music is, it will never sound right! And not only will it not sound perfect, some of it will sound pretty nasty if you’re not extra careful.
We will not go into much more detail. At this point, you came to realize that when cutting an octave into 12 notes to produce the standard European scale, you have to make trade-offs: if you want some intervals to sound close to prefect, some other intervals will have to be sacrificed. Some fifths will not be exact 3/2 intervals. Some thirds will be really off from their exact intervals. Mostly everything will be off, really, ever so slightly. The goal is to find a slicing that minimizes the roughness in the ear coming from all these intervals that are off. Pythagoras showed that you could tune most notes almost perfectly but that you would then have an inevitable rogue interval that would sound so terrible that it is called a “Wolf interval” since it howls like a wolf when you hear it!
Many musicians since Pythagoras have tried to address the problem in one way or another, designing “the best slicing” of their choice. These different variations in slicing the octave cake are called “temperaments”. If you know a little about classical music, this could remind you of the title of J.S. Bach’s “Well-Tempered Keyboard”. In the 18th century, there were many different temperaments, each suffering from various problems when playing in different keys, such as the Werckmeister and the Valotti cited in the prologue of this article. Bach’s work “The Well-Tempered Keyboard” uses many intervals in order to give a practical demonstration of his temperament in which you could play in various keys without problem and without hearing any wolf interval.
Besides, with a given temperament, musicians started to understand that every key had a different “mood”, some sad, some scary, some joyful, due to the different parts of the melody that sounded rounder or harsher than the others depending on which intervals they were using most. Therefore, they chose the keys of their compositions very carefully.
Here is an example of a classification from various composers such as Charpentier or Rameau:
- C major: joyful
- C minor: sad, mourning, love sorrow
- D major: funny, triumphant, victory
- D minor: calm, grave, tender, devotion
- E flat major: pathetic, cruel, harsh, devotion
- E flat minor: horrible, anxiety
- ..
- F major: storm, furious
- etc.
Nowadays, one temperament is used almost universally (except for baroque players, mostly): the “equal” temperament. It has actually been invented some centuries ago (in fact, a Chinese mathematician described it around 400 AD), but it can be tuned perfectly only with the precision of electronic devices (although there are methods to reach very good approximations of it, people began to use it in the 18th century). Rather than making compromises, the equal temperament makes every single interval as equally good/bad as the others. Basically, the octave is cut into 12 absolutely equal pieces. This is why some musicians criticize it and why it faced some resistance before being adopted: it has no “color”. Whether you play your tune in C or in G flat, it will sound exactly the same, at a different pitch, but with the same harmonics. In other temperaments, as we have seen, every key has its own “mood”. You may not even be able to play some keys in some temperaments because they will sound hideous, as if you were playing on one of those out of tune pianos in the pubs of the 1900s. But in equal temperament, nothing sounds exactly right at all, it is just never totally hideous either. In fact, in the equal temperament, no single interval is perfect, except for the octave.
This is it for a very short introduction to music theory of temperaments. Many books have been written on the subject, and it is still not over as people still come up with new ideas to get the best compromises out of a scale. I hope this has intrigued you and made you wonder a little more about this simple problem that has annoyed musicians for thousands of years.
For some examples of how a temperament can affect how you hear things, you can have a look at the Wikipedia page for musical tuning and listen to the samples in the “Systems for the twelve-note chromatic scale” section, the “just intonation” is particularly telling!