I’ve been using spaced repetition for quite some time now. My favorite program is Anki, even if I have also tried a few others. I had actually developed one myself before I even knew the SuperMemo algorithm existed back in the late 1990’s, that was more than 10 years before the first Anki release.

Interestingly, spaced repetition has been around since the democratization of computers. That’s for a reason: spaced repetition is very easy to do on computers, but not so easy with physical supports. Although Piotr Wozniak, the inventor of Spaced Repetition, used paper to do his studies, he switched to a computerized version as soon as he got a computer. I have been wondering for a while how it could be achieved without too much hassle from the user’s point of view. I finally came up with what I find a rather easy and elegant solution.

The problem with regular flashcards

Who didn’t try to make paper cards of things they wanted to remember? You write a question on the front side, the answer on the back side. It could be anything, including pictures. When picking that card, you have to remember the answer. By repeating the process, you’ll learn that information, eventually.

However, without a planned schedule, that process is very inefficient. You often get exposed to cards that you already know perfectly, which is frustrating, especially if there are so many of them. The sensation that you’re losing your time is taking over. Then you’re tempted to put them away for good. Only to realize a few months later that you forgot the information they hold. Similarly, you sometimes get exposed to cards that you have already forgotten.

This is why Spaced Repetition has been invented: it is optimizing the interval at which you are exposed to the different cards.

Spaced Repetition principles

So, just as a reminder, what is Spaced Repetition?

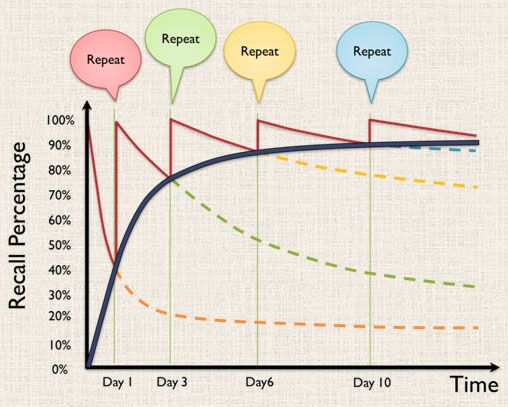
Basically, it is taking advantage of how our memory works. When exposed to some information for the first time, the brain forgets it very fast. It could be just an hour or a day. Then it filters this information out, to give space to new information. But when exposed to this information again before it is wiped out, the brain starts giving some bigger importance to it. Thus it will remember it longer. Maybe 2 or 3 days.

Again, after a few days, that information will be deleted. Unless you get exposed to it again before it is erased, in which case it will get an even stronger importance. This time, the brain will remember it for a week or two. And so on. Basically, every time you remember that information before it gets deleted, the brain sort of doubles its importance. This means that it will take double the time before it forgets it. “Double” is a rough estimate, the actual rate varies from person to person, and heavily depends on the knowledge to be learned itself, along with the eagerness of the learner.

So the goal is to be exposed to the information at increasing intervals. The key being that the information should reappear before it is erased from your memory.

Attempts

There are people who have attempted to do that. Of course, the inventor himself came up with tables where he marks the intervals.

Although it works, it uses up some paper, and you need a cache to cover the words that need to be learned.

Other people have invented something which is closer to my goal. The idea is to have several boxes, each one of them contains a different interval. The first time you’re exposed to a card, you’ll put it in the first box, which is the daily interval. Once it is learned, it goes to the second box, which could be the weekly interval. And so on.

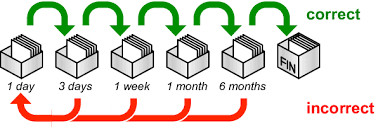There is still a problem with this method: if you pick cards from the weekly box every Sunday, then you’ll pick cards from Saturday, which is not good.

In other words, the question is: how do you know how many cards to pick from the weekly box and when to pick them? How do you know 7 days have really passed since that card was put in the box? You don’t know. Which can cause problems. Especially when moving to longer intervals.

Thinking of a board

I thought about developing a board on which it would be easy to know when to pick cards, especially on longer intervals.

Just like the boxes, the goal is to have several zones on the board, with increasing intervals. Thus when remembering a card in a certain zone, it is then moving up to the next zone. This way, the intervals for a card are increasing, similar to the boxes.

Furthermore, for a card in a long interval zone, we can add markers to show where we are in the interval. Luckily, it is not difficult to make markers.

Additionally, everything depends on the size of the cards you want. I chose the “compact” route, with cards that are square and not bigger than an inch (actually 2 cm in my prototype). But of course, the same principle could just be used with bigger cards, it would simply take more space.

The final result and its explanations

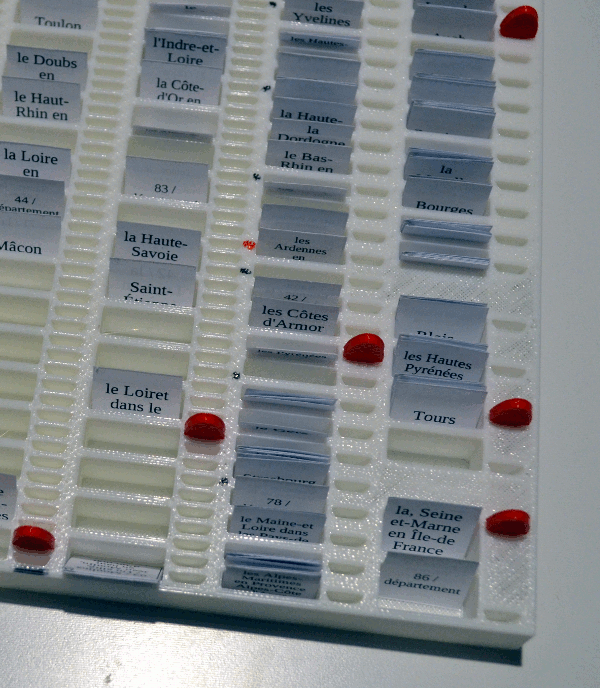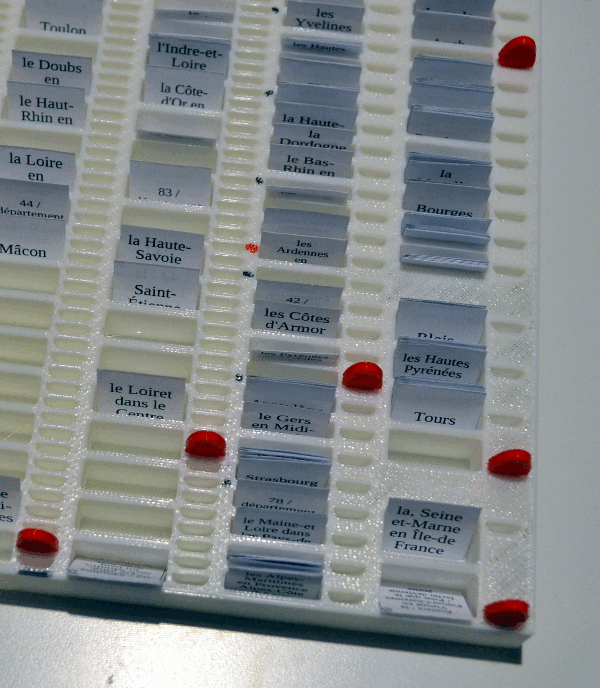
Here is the model of the board I have come up with, which I then printed with a 3D printer.

The column on the right represents the shortest intervals. Every column has two parts: the left part with larger holes in which the cards can be kept, and the right part that contains small holes in which little pegs can be inserted. These pegs are the markers that help keep track of where we are in time.

Moving Pegs

Basically, you just move every peg one step further. They show you directly which cards need to be reviewed that day. Here is what happens when you start a new day:

For the longest intervals, the pegs are moved forward only when the last daily peg reaches one of the marked spots, as seen in this picture:

This way, the two last columns move forward only when the “Daily Move” column reaches one marked spot. This happens every week and every month, respectively.

Note that the last 3 columns have more “peg holes” than “card holes”. Therefore, you don’t need to review cards in these three columns right away when the peg comes to a new spot with cards. Instead, you can pick them gradually, for instance on less busy days.

Learning cards

Every day, you pick cards from the spots that are marked by the pegs. If you forgot the contents of the card, then that card goes back to daily learning, at the bottom right of the board.

If you did remember what was on a card, then you can move it to the next zone, just behind the next zone’s marker. This way, you will have to wait a full cycle of the marker to review that card again.

Here is the representation of the movements of the cards, according to the current peg positions on that board:

Conclusion

This board, which I have already been using for a while now, is very convenient for spaced repetition without the need of a computer. It is quite compact, in fact I have calculated that it could hold no less than 5000 cards. Of course, other boards can be printed if this is not sufficient! It still needs to get a decent cover so that it could be easily transportable.

The board is available to print on Thingiverse: https://www.thingiverse.com/thing:3974248

It is also available on my gitlab: https://gitlab.com/jytou/3d-paper-spaced-repetition

I have also written a converter to print your anki decks: https://gitlab.com/jytou/anki2papergenerator

Cher lecteur, si tu connais déjà tout sur le système majeur, tu peux sauter directement à la solution. Pour les autres, vous apprendrez quelque chose en lisant l’article en entier ! Et pour les plus impatients, la page web est là : https://jytou.fr/majeur/?n=15

Pour la plupart des gens, mémoriser des grands nombres est un défi qui s’arrête très vite. À grand peine, on arrive avec le temps à mémoriser des grands nombres par la répétition, année après année, comme le numéro de sécurité sociale ou les numéros de téléphone, qu’on arrive généralement à mémoriser seulement le jour où on en change.

Le système majeur

Et pourtant, nous avons à notre disposition des méthodes qui permettent de mémoriser des grands nombres, dont une très populaire qui fonctionne par associations de sons : le système majeur, parfois aussi appelé « Grand Système » en français. Nous devrions tous apprendre cette méthode à l’école ! Cette méthode peut être utilisée dans beaucoup de langues avec quelques modifications basiques. Et pourtant, quel pourcentage de la population connaît cette méthode ? Combien l’utilisent vraiment ? Le pourcentage doit se compter sur les doigts d’une main.

Pour résumer, il s’agit juste de trouver des mots dont les consonnes prononcées correspondent aux chiffres à retenir. Par exemple, pour le chiffre « 0 » on cherchera un mot avec un son « s » ou un « z », pour un chiffre « 1 » on aura un « t » ou un « d », etc.

Voilà le tableau des correspondances généralement utilisées pour la langue française :

Nombre	Lettre	Associations visuelles
0	s, z	Le chiffre 0, zéro, produit un son sifflant.
1	t, d	Un seul trait vertical
2	n	Deux traits verticaux
3	m	Trois traits verticaux
4	r	La lettre r se retrouve dans quatre en français, four en anglais, vier en allemand, etc.
5	l	La lettre L ressemble au chiffre romain L (50)
6	j, ch, sh	La lettre j manuscrite ressemble à un 6 inversé
7	k, c, g	La lettre K ressemble à deux 7 accolés. G est phonétiquement proche de k.
8	f, v, ph	Deux lettres f ressemblent à un 8. V est phonétiquement proche de f et de ph.
9	p, b	La lettre P ressemble à un 9 inversé. P et b sont phonétiquement proches.

Bien évidemment, il ne s’agit que de conventions et comme l’apprentissage est très personnel, chacun peut faire des choix différents quant aux correspondances. En revanche, chaque changement nécessite de se poser de nombreuses questions : en choisissant telle correspondance, ne vais-je pas me retrouver dans des situations difficiles parce que je n’avais pas prévu que telle lettre n’est pas très présente dans la langue, par exemple ? Dans tous les cas, chaque changement doit être mûrement réfléchi et résister à l’épreuve de la pratique.

Une fois les conventions adoptées, il s’agit de les tester avec des cas concrets et des chiffres à retenir. L’un des défis est de trouver rapidement des mots correspondant aux chiffres puis de les assembler en une suite de mots qui veut dire quelque chose, même si c’est un peu loufoque. D’ailleurs, plus c’est loufoque, plus ce sera facile à retenir. Nous mémorisons ce qui fait appel à l’émotion et à l’imagination. Si c’est trop « plat », on oublie tout de suite.

Tables apprises par cœur

Pour gagner du temps, une technique courante consiste à mémoriser des mots déjà tout prêts pour des combinaisons de deux chiffres, comme 10=tasse, etc. Voici un exemple d’un tel tableau, qu’on appelle « table de rappel » :

	0 s, z	1 t, d	2 n	3 m	4 r	5 l	6 j, ch	7 k, g	8 f, v	9 p, b
0 s, z	0 as	10 tasse	20 nasse	30 masse	40 race	50 lasso	60 chasse	70 casse	80 face	90 passe
1 t, d	1 tas	11 tata	21 natte	31 maths	41 rate	51 latte	61 château	71 cata	81 fête	91 patte
2 n	2 nez	12 tanin	22 nana	32 manne	42 reine	52 laine	62 chaîne	72 canne	82 fan	92 panne
3 m	3 mât	13 tamis	23 nem	33 maman	43 rame	53 lame	63 chameau	73 came	83 femme	93 pomme
4 r	4 rat	14 tare	24 nerf	34 mare	44 rare	54 lard	64 char	74 car	84 phare	94 part
5 l	5 la	15 talus	25 nylon	35 mâle	45 râle	55 lolo	65 châle	75 cale	85 fil	95 pelle
6 j, ch	6 chat	16 tache	26 niche	36 machin	46 ruche	56 lâche	66 chéchia	76 cache	86 facho	96 pacha
7 k, g	7 cas	17 taquin	27 nuque	37 mac	47 rack	57 laque	67 chèque	77 caca	87 fac	97 pack
8 f, v	8 feu	18 tif	28 nef	38 mafia	48 raffut	58 louve	68 chef	78 café	88 fief	98 pif
9 p, b	9 pas	19 tape	29 nappe	39 myope	49 râpe	59 lapin	69 chapeau	79 cape	89 fip	99 papa

Certains vont même jusqu’à mémoriser 3 chiffres, soit 1000 mots à associer aux 1000 premiers nombres. Bien sûr, c’est très utile pour ceux qui en font un grand usage comme les champions des concours de mémorisation. En revanche, pour les autres, c’est beaucoup de sport cérébral qui finalement risque de ne pas servir à grand-chose, à part peut-être pour briller occasionnellement en société. De manière générale, le tableau ci-dessus suffit pour un usage occasionnel. Pour ma part, je préfère mémoriser trois mots au lieu d’un pour chaque paire de chiffres : un nom, un adjectif et un verbe. Cela permet de faire des phrases qui se retiennent beaucoup plus facilement. L’inconvénient est une petite perte de temps à choisir le mot pour chaque paire afin de former une phrase.

Voyons comment ça se passe dans la pratique avec un exemple.

Défis

Tentons de mémoriser 15807020 avec la table présentée au-dessus :

15	80	70	20
talus	face	casse	nasse

Avec ces mots, on peut facilement faire une phrase qui utilise tous ces mots dans l’ordre, en se rappelant que seuls les noms, adjectifs et verbes sont importants et que le reste compte pour du beurre : « Un talus en face, tu casses ta nasse ». Pour retrouver le nombre, il suffit de se rappeler de cette phrase puis reprendre les noms et les codes de chaque lettre. C’est une technique simple, mais il reste encore à mémoriser cette phrase, ce qui n’est pas toujours évident. Surtout que, dans certains cas, c’est beaucoup moins évident de faire une phrase avec : chameau, lame, panne, mâle. Pas de verbe, pas d’adjectif. Un bon petit casse-tête.

Aller plus loin

Dans le cas d’une mémorisation rapide, il est préférable d’utiliser une table comme celle qui vient d’être présentée. En revanche, pour des mémorisations où on a tout notre temps pour élaborer une technique, il est préférable d’optimiser un peu. Plutôt que d’utiliser des « mots tout prêts », on va chercher des mots plus longs, une phrase facile à retenir et qui fait sens plutôt que des mots imposés.

L’un des défis avec ce système est de trouver rapidement des mots « mémorables » et qui se combinent bien pour une certaine combinaison de chiffres. Or, lorsqu’on se retrouve face à 15807020, il n’est pas toujours évident de trouver des mots assez longs pour rivaliser avec la simple mémorisation des mots à 2 chiffres. Sans entraînement, on peut y passer beaucoup de temps. Et même avec de l’entraînement, la combinaison que l’on trouve est souvent loin d’être optimale.

Parfois, il peut aussi être intéressant de former une suite de mots directement à partir du nombre à mémoriser avec des mots de taille variable. Par exemple, pour mémoriser 15807020, on pourrait se rappeler de suite de mots suivante :

Télé visqueuse et niaise
tele visk ø z  e  njɛ z
1 5  8 07   0     2   0

Facile de se faire une image mentale de cette phrase, il suffit d’avoir un peu d’humour.

Sans aucun doute, il est plus facile de mémoriser moins de mots choisis dans le vocabulaire courant plutôt qu’une grille fixe. Par ailleurs, leur longueur n’a aucune importance car, dans la tête, un mot est une entité mémorisable directement quelle que soit sa longueur, comme on l’a fait plus haut avec la télé visqueuse et niaise.

Il existe déjà un excellent logiciel nommé 2know qui permet de trouver tous les mots correspondant à une suite de chiffres donnée. Malheureusement, je trouve cette application un peu trop limitée car on ne peut chercher qu’un seul mot à la fois. Il faut alors tester toutes les combinaisons pour trouver des mots adéquats. Par ailleurs, ce logiciel ne fonctionne que sous Windows, même s’il est utilisable sous linux et wine, c’est loin d’être idéal.

La solution

Par conséquent, j’ai développé une page internet qui permet de donner toutes les combinaisons de mots qui peuvent se rapporter à une suite de chiffres. L’avantage est que l’on ne dépend pas de la plateforme, elle peut être visitée et utilisée à partir de n’importe quel terminal informatique pour peu qu’il dispose d’un navigateur.

Lorsqu’on lui présente un nombre, elle calcule toutes les possibilités de mots qui peuvent être trouvés avec la suite de chiffres en question. Ainsi, elle affiche les possibilités dans un tableau. Les mots les plus longs sont placés en haut du tableau puisque ce sont eux qu’on va choisir préférentiellement, chaque ligne est ensuite complétée avec les mots plus petits. On peut ainsi voir les possibilités intéressantes de combinaisons de mots. Par ailleurs, la page affiche également les mots par type grammatical, car il peut être pratique d’enchaîner un nom, un adjectif, un verbe puis finalement un nom pour former une phrase syntaxiquement correcte.

Il suffit de naviguer là pour voir comment cela fonctionne : https://jytou.fr/majeur/?n=15807020

On retrouve facilement la télé visqueuse et niaise, mais on peut également inventer d’autres combinaisons très rapidement.

Quelques petits réglages peuvent être paramétrés comme le style plutôt noir sur fond blanc ou l’inverse et le tri des mots. La page reste très simple et épurée de toute distraction.

Et après ?

À l’origine, je visais un peu plus compliqué. J’envisageais que la page fasse également des suggestions de phrases, en utilisant des règles simples permettant de prendre des mots à la suite ayant de fortes chances de faire des phrases correctes. On peut imaginer par exemple : interjection, article/démonstratif…, nom, adjectif, verbe, nom, adjectif. Et ainsi de suite. Pour l’instant, la page telle qu’elle est me suffit – le rasoir d’Okham a encore frappé ! N’hésite pas à commenter si la page plus élaborée t’intéresse et si celle-ci te sert déjà à quelque chose !

Pour les techniciens…

Pour ceux qui se posent la question du développement de cette page, j’ai récupéré le dictionnaire du français avec classification grammaticale et phonétique ici : https://github.com/WhiteFangs/lexique.sql

Ce lexique est issu du projet suivant : http://www.lexique.org/

Il contient 150.000 mots, du pain bénit ! J’ai fait un petit peu de ménage dans la classification et gardé seulement le strict nécessaire dans la table SQL, c’est-à-dire l’orthographe, la phonétique, la correspondance en système majeur, la classification grammaticale ainsi que le masculin/pluriel et la fréquence du mot pour afficher les mots les plus courants en premier. En effet, il est d’autant plus facile de mémoriser un mot dans une suite qu’il est utilisé couramment.

Ensuite, il m’a fallu faire un petit programme java pour calculer et stocker en base de données la correspondance entre prononciation et équivalent en système majeur.

Enfin, une page en PHP permet de faire la recherche des mots qui correspondent au nombre recherché et les affiche dans un tableau, simple comme bonjour !

Category: Memorization

A Board for Paper-Based Spaced Repetition Memorization