Note : English version of this article here.
Avertissement : cet article traite de théorie de la musique, expliquée simplement aux musiciens ainsi qu’aux non musiciens, avec des mathématiques élémentaires (en utilisant des fractions simples). Le sujet est en fait assez méconnu, même des musiciens. À moins que vous ne sachiez ce que sont Werckmeister et Valotti, vous apprendrez quelque chose d’intéressant !
Depuis que la musique existe, les musiciens doivent accorder leurs instruments pour éviter de casser les oreilles de leur audience. Ce n’est pas seulement valable pour un orgue aux 20.000 tuyaux. L’un des instruments les plus simples, une flûte de bambou (ou d’os, quoi de plus romantique que de jouer son air préféré sur le tibia de votre chérie ? je plaisante…) avec des trous doit être construite avec minutie : un millimètre à côté, votre flûte sonnera faux.

Il y a 2500 ans, Pythagore, avec les quelques instruments simples dont il disposait à son époque, se cassa la tête sur les mystères de l’accord des instruments et créa le désormais célèbre « cycle des quintes », exposant l’impossibilité d’accorder parfaitement un instrument, quel qu’il soit :
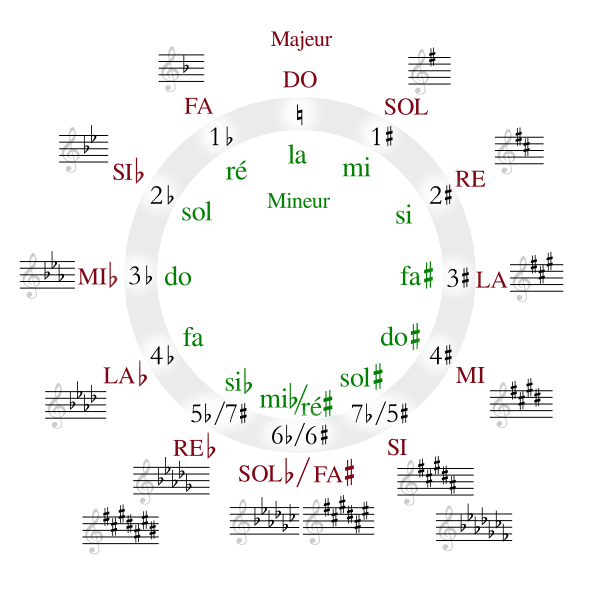
Pythagore comprit que la musique est essentiellement des mathématiques : les notes, les harmonies, la tonalité, les octaves, sont faites de fréquences et de la manière dont ces fréquences interagissent. Nos cerveaux et oreilles analysent les fréquences qui ont des relations mathématiques particulières entre elles comme harmonieuses, et les autres comme dissonantes. En réalité, le cerveau aime tout ce qui est mathématiquement « beau ». C’est la raison pour laquelle nous adorons les symétries telles que celle-ci :

Revenons à la musique. Lorsque deux notes sont jouées simultanément, elles forment un « intervalle », qui est la distance entre leurs fréquences sonores respectives. Un intervalle est agréable à l’oreille lorsque les fréquences des deux notes qui le composent sont mathématiquement liées par une fraction entière. Dès que les fréquences des deux notes s’éloignent d’une telle relation mathématique, l’intervalle sonne faux, il casse les oreilles. D’ailleurs, un intervalle qui s’éloigne de cette perfection mathématique se met à créer des interférences et à « battre », ce qui est très pratique pour accorder des intervalles avec précision sur un instrument de musique. L’oreille est un organe très délicat et très précis.
Laissons la théorie pendant un instant et faisons un peu de pratique ! J’ai enregistré une quinte (5 notes d’écart sur un clavier de piano), l’intervalle Do-Sol sur mon épinette. L’épinette est un petit clavecin qui n’a qu’une seule corde par note, ce qui rend les choses plus faciles à entendre. Pour commencer, écoutons une quinte parfaitement accordée. Elle sonne juste, et surtout le son est régulier, il diminue d’intensité progressivement et sans à-coups (il est préférable d’utiliser un casque) :
Visuellement, le son ouvert dans un logiciel permettant de voir la forme des sons est une courbe descendante sans grande particularité :

Maintenant, désaccordons très légèrement le sol. L’accord se met à « battre », comme le montre la vidéo suivante. N’hésitez pas à la réécouter en suivant l’indication visuelle, jusqu’à ce que vous entendiez ces vagues qui font « wow, wow, wow… » :
Et lorsqu’on regarde la forme du son, les battements sont déjà visibles :

Désaccordons encore un peu plus le sol. Les battements sont plus rapides. À noter que ce n’est pas un effet digital, l’épinette sonne réellement exactement comme ça :
Cette fois, la forme du son indique très clairement ces battements :

Et pourtant, la seule chose que nous ayons fait ici est de changer très légèrement le sol, le faisant dévier de moins de 1% de sa valeur parfaite !
Regardons maintenant les différents intervalles qui peuvent être formés.
| Prenons une fréquence et son double, on obtient une octave. Par exemple 440 Hz et 880 Hz. |  |
| Prenons les 3/2 d’une fréquence, on obtient une quinte parfaite. |  |
| Les 4/3, une quarte. |  |
| Les 5/4, une tierce majeure. |  |
| Les 6/5, une tierce mineure. |  |
Dès que deux notes ne suivent pas ces intervalles précis, leur combinaison sonne faux et l’intervalle commence à « battre ».
Pour l’instant, tout va bien. Avec ce qu’on vient de voir, on pourrait tout simplement dire qu’il ne nous suffit plus qu’à accorder notre instrument avec des intervalles parfaits, et le tour est joué !
Sauf qu’en réalité, c’est là qu’intervient le problème : il est mathématiquement impossible de découper une octave en douze notes (les demi-tons) de manière à obtenir des quintes parfaites, sans même parler de quartes ou tierces parfaites. Pourquoi donc ? Ne nous en tenons pas à cette affirmation péremptoire, démontrons-la.
Une octave parfaite sonne généralement très bien. C’est la combinaison d’une fréquence et de son double, le cerveau est pleinement satisfait de la perfection mathématique qui en résulte. D’ailleurs, lorsqu’elle est parfaitement accordée, il est même parfois difficile d’entendre deux notes distinctes tellement elles se marient impeccablement. Arrivez-vous à entendre deux notes distinctes de cette octave enregistrée sur mon épinette ?
Avec son cycle des quintes, Pythagore, qui avait décidément d’autres choses en tête que des triangles, montra que, si on voulait accorder un instrument avec des quintes parfaites, les octaves que l’on obtiendrait sonneraient comme cela :
Ouille ! Vous allez avoir besoin de vous gratter les oreilles après une telle horreur. Je vous invite à réécouter l’octave parfaite au-dessus pour rétablir un certain calme dans votre oreille et votre cerveau agacé par autant d’imperfection.
Pythagore utilisa de nombreuses quintes et octaves pour faire sa démonstration, mais nous pouvons nous contenter de 5 notes pour aboutir au même résultat.
Calculons la différence entre un do et un ré de manière à avoir des notes parfaites. Do-sol est une quinte, c’est donc un intervalle 3/2 comme nous l’avons vu dans la table précédente. Cela veut dire que la fréquence du sol est 3/2 plus grande que la fréquence du do. D’autre part, ré-sol est une quarte, elle doit donc suivre un intervalle 4/3. Ce qui signifie que pour passer du sol au ré, nous devons diviser par 4/3.
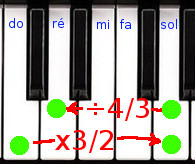
sol = do × 3/2
ré = sol ÷4/3 = sol × 3/4 = (do × 3/2) × 3/4 = do × 9/8
Ré est donc 9/8 de la fréquence de do si on veut avoir des intervalles parfaits. Excellent ! Ce ne sont là que des mathématiques simples, passant d’une note à l’autre à l’aide de fractions.

Calculons maintenant la différence entre do et mi. Facile. Do-ré est un ton, ré-mi est également un ton, il y a donc également 9/8 entre ré et mi.
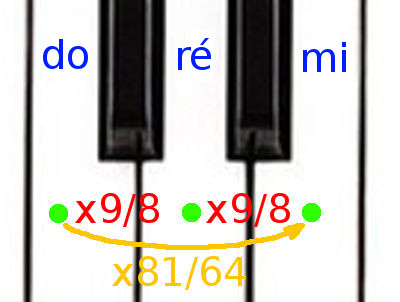
Ce qui veut dire que, pour passer de do à mi, il suffit de multiplier par le carré de 9/8, soit 81/64. Et 81/64 ≈ 1,265.
Une petite seconde ! Do-mi est une tierce majeure. Nous avons vu dans la table plus haut que les tierces majeures parfaites suivent un intervalle de 5/4. Mais 5/4 est égal à 1,25, pas 1,265. Pas loin. Mais pas exactement identique. Voilà notre première déception : si on veut construire ré de manière à avoir des intervalles justes, alors notre tierce do-mi ne peut pas être parfaite. On peut déjà imaginer que ce qui est vrai pour cette tierce va être également valable pour bien d’autres intervalles.
Par exemple, essayons de reconstruire une octave avec notre gamme composée de tons valant 9/8 chacun. Do-ré est 9/8, do-mi est 9²/8² (9/8 fois 9/8), do-fa# est 9³/8³, etc. :
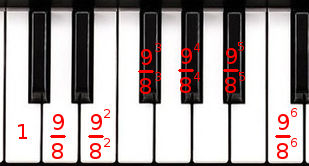
Une octave composée de 6 tons est donc 9⁶/8⁶ ≈2,0273. Nous avons vu qu’une octave doit avoir un ratio d’exactement 2 pour être parfaite, pas 2,0273. Et voilà comment la perfection en musique disparaît sous nos yeux ou plus exactement nos oreilles. Et vous avez déjà entendu à quoi ressemble une octave à 2,0273 au lieu de 2, c’est tout simplement horrible ! Écoutons-la encore :
Il nous faut donc accepter un fait qui est dur à avaler : diviser une octave en douze notes ne va jamais nous permettre d’obtenir des quintes, quartes et tierces exactes. Des approximations très proches, mais jamais exactes. Quelle que soit la manière dont vous allez accorder votre instrument, il ne produira jamais d’harmonie parfaite. Quelle pensée agaçante pour un musicien ! Aussi parfaite que soit sa musique, elle sonnera toujours faux ! Et d’ailleurs, si l’on n’est pas extrêmement vigilant, certaines portions risquent même de casser sérieusement les oreilles.
Nous n’allons pas rentrer dans davantage de détails. L’essentiel est d’avoir compris que la perfection en musique est tout simplement inatteignable, et que pour produire 12 notes dans une octave européenne, il faut faire des compromis : si l’on veut que certains intervalles soient presque parfaits, il va nous falloir en « sacrifier » certains autres. Plus les uns sonneront à la perfection, plus les autres sonneront faux. Alors, certaines quintes ne seront pas exactement de 3/2, des quartes et tierces dévieront sensiblement de leur ratio parfait. En fait, tout va sonner un peu faux. Le but de l’accordeur et du compositeur est de minimiser les frictions dans l’oreille venant de ces imperfections. Pythagore a montré qu’on peut effectivement accorder la majeure partie d’un instrument de manière presque parfaite, mais qu’on obtient alors inévitablement un intervalle atroce qui sonne terriblement faux qu’on appelle typiquement « la quinte du loup », tellement cet intervalle sonne comme le hurlement d’un loup.
Depuis Pythagore, de très nombreux musiciens ont tenté de trouver une solution à ce problème, d’une manière ou d’une autre, découpant l’octave en 12 notes de manières toutes plus ingénieuses les unes que les autres. Ces différentes variations, ces différents découpages, sont appelés « tempéraments ». Cela peut évoquer aux amoureux de musique classique le titre de l’œuvre de J.S. Bach « Le clavier bien tempéré ». Au XVIIIème siècle, il existait de nombreux tempéraments, chacun avec ses avantages et inconvénients, la plupart n’autorisant pas de jouer dans certaines tonalités, comme le Werckmeister et le Valotti que j’ai cités en début d’article. L’œuvre de Bach « Le clavier bien tempéré » utilise de très nombreux intervalles pour montrer de manière pratique les applications du tempérament qu’il avait développé et qui permettait de jouer dans n’importe quelle tonalité sans problème et sans être gêné par une quinte du loup.
D’autre part, dans chaque tempérament, les musiciens réalisèrent que chaque tonalité avait sa propre « humeur », certaines tristes, d’autres joyeuses, d’autres encore inspirant l’angoisse, à cause des différents intervalles majoritairement utilisés dans chaque tonalité qui sonnent plus ou moins juste. Du coup, ces musiciens se mirent à choisir très précisément la tonalité et le tempérament de leurs compositions en fonction de l’atmosphère qu’ils voulaient leur donner.
Voici un exemple de classification par différents compositeurs comme Charpentier ou Rameau:
- Do majeur : joyeux
- Do mineur : triste, deuil, chagrins amoureux
- Ré majeur : drôle, triomphant, victorieux
- Ré mineur : calme, grave, tendre, dévot
- Mi b majeur : pathétique, cruel, sévère, dévot
- Mi b mineur : horrible, anxieux
- …
- Fa majeur : tempête, furieux
- etc.
De nos jours, un tempérament particulier est devenu la référence pour presque tout le monde (excepté la musique baroque et renaissance, principalement) : le « tempérament égal ». Il fut inventé il y a plusieurs siècles et même décrit autour de 400 de notre ère par un mathématicien chinois, et bien que des méthodes existent depuis le XVIIIème siècle pour l’accorder à l’oreille, il ne peut être réellement atteint qu’à l’aide de la précision des instruments électroniques. Ce tempérament, plutôt que de faire des compromis et favoriser tel ou tel intervalle, rend chaque intervalle aussi bon/mauvais que les autres. Il consiste simplement en un découpage de l’octave en 12 parts parfaitement égales. Son acceptation n’a pas été facile et certains musiciens le critiquent encore aujourd’hui : il n’a pas de « couleur ». Que vous jouiez votre morceau en do ou en sol# n’a aucune importance, il sonnera toujours pareil, à une hauteur différente, mais avec les mêmes harmonies. Dans tous les autres tempéraments, comme on a pu le voir, chaque tonalité a sa propre « humeur ». Il est même parfois impossible de jouer dans certaines tonalités parce que cela sonne horriblement faux, comme si on jouait sur un de ces pianos désaccordés des bars des années 1900 aux États-Unis. En tempérament égal, rien ne sonne parfaitement juste mais rien ne sonne totalement faux non plus. Aucun intervalle n’est parfaitement juste à part les octaves. Notre oreille s’y est habituée avec le temps mais l’expérience d’écouter d’autres tempéraments peut parfois être une vraie révélation pour certains. Tout dépend de votre oreille, de vos attentes, de votre envie de découvrir autre chose, etc.
Nous allons nous arrêter là pour cette rapide introduction sur les tempéraments en musique. C’est un sujet qui a fait couler beaucoup d’encre et alimenté les conversations pendant des millénaires. Et c’est loin d’être terminé car des gens se penchent toujours sur le problème, tentant des nouvelles approches pour découper l’octave de différentes manières par des compromis différents, frustrés par la totale imperfection du tempérament égal. J’espère que cet article vous aura intrigué, vous aura fait approcher la musique sous un angle différent et montré ce problème pourtant simple qui agace les musiciens depuis que la musique existe.
Pour des exemples sur la manière dont différents tempéraments affectent la sonorité de la musique, vous pouvez vous rendre sur la page wikipedia (en anglais, mais il suffit de cliquer sur les boutons ► à droite, on entend clairement les intervalles qui sont vraiment faux, le premier exemple en “just intonation” est particulièrement horrible dans certains passages).

One thought on “Ce problème simple qui défie les musiciens depuis des millénaires”